K-Means Clustering

MATH/COSC 3570 Introduction to Data Science

Dr. Cheng-Han Yu
Department of Mathematical and Statistical Sciences
Marquette University

Clustering Methods

• Clustering: unsupervised learning technique for finding subgroups or clusters in a data set.

• GOAL: Homogeneous within groups; heterogeneous between groups

• When we group data points together, we hope the points in the same group look very much like each other, and the points in the different groups or clusters look very different.
• When I say they look like each other, I mean the points share similar characteristics. In other words, their variables’ values are pretty similar.

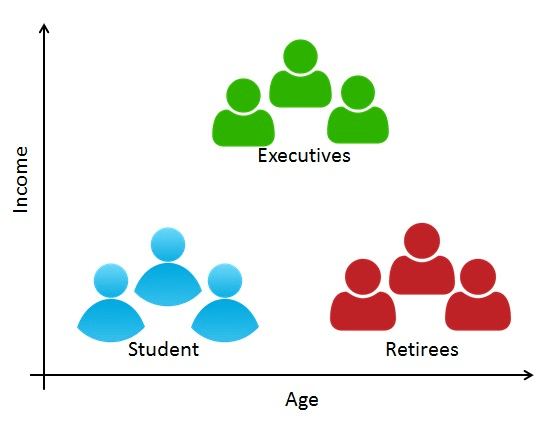
• Customer/Marketing Segmentation
  • Divide customers into clusters on age, income, etc.
  • Each subgroup might be more receptive to a particular form of advertising, or more likely to purchase a particular product.

Source: https://www.datacamp.com/community/tutorials/introduction-customer-segmentation-python

• Divide customers into clusters on the basis of common characteristics.
• Students: the price shouldn’t be that high, and the item should be good-looking and maybe colorful, so it looks young.
• If we target this group, the low price is not that important, but the item should be beautiful, high-class and high quality.

K-Means Clustering

• Partition observations into \(K\) distinct, non-overlapping clusters: assign each to exactly one of the \(K\) clusters.

• Must pre-specify the number of clusters \(K \ll n\).

Source: Introduction to Statistical Learning Fig 12.7

• A data point cannot belong to two clusters at the same time.
• As KNN, we have to decide how many clusters the data are partitioned into.

K-Means Illustration

Data (Let’s choose \(K=2\))

K-Means Algorithm

• Choose a value of \(K\).
• Randomly assign a number, from 1 to \(K\), to each of the observations.
• Iterate until the cluster assignments stop changing:
  • [1] For each of the \(K\) clusters, compute its cluster centroid.
  • [2] Assign each observation to the cluster whose centroid is closest.

K-Means Illustration

Random assignment

K-Means Algorithm

• Choose a value of \(K\).
• Randomly assign a number, from 1 to \(K\), to each of the observations.
• Iterate until the cluster assignments stop changing:
  • [1] For each of the \(K\) clusters, compute its cluster centroid.
  • [2] Assign each observation to the cluster whose centroid is closest.

K-Means Illustration

Compute the cluster centroid

K-Means Algorithm

• Choose a value of \(K\).
• Randomly assign a number, from 1 to \(K\), to each of the observations.
• Iterate until the cluster assignments stop changing:
  • [1] For each of the \(K\) clusters, compute its cluster centroid.
  • [2] Assign each observation to the cluster whose centroid is closest.

K-Means Illustration

Do new assignment

K-Means Algorithm

• Choose a value of \(K\).
• Randomly assign a number, from 1 to \(K\), to each of the observations.
• Iterate until the cluster assignments stop changing:
  • [1] For each of the \(K\) clusters, compute its cluster centroid.
  • [2] Assign each observation to the cluster whose centroid is closest.

K-Means Illustration

Do new assignment

Compute the cluster centroid …

Source: Introduction to Statistical Learning Fig 12.8

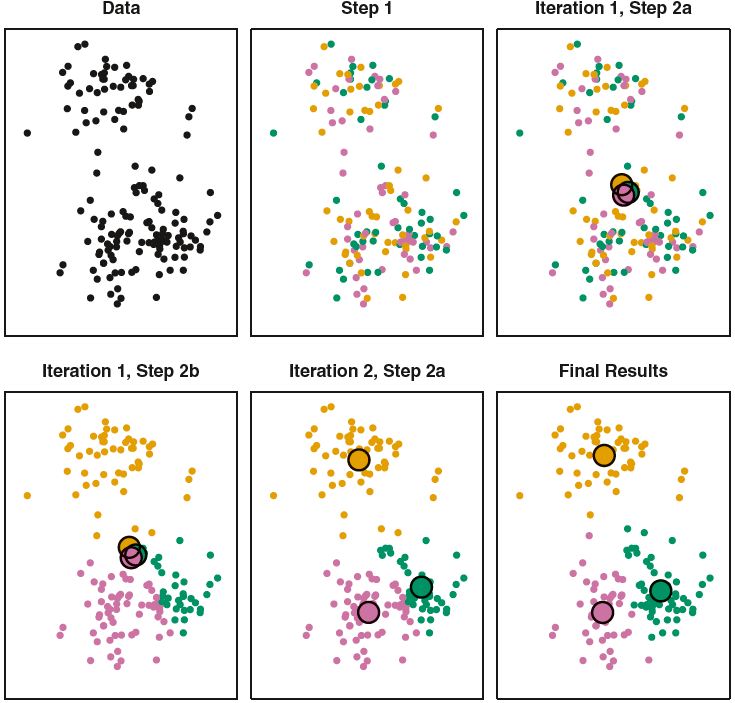
K-Means Algorithm

Note

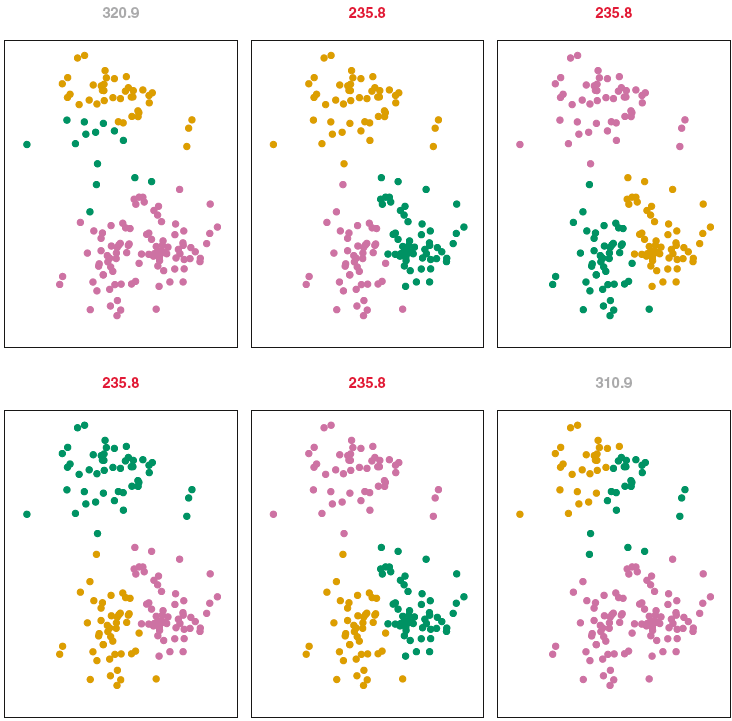
• The K-means algorithm finds a local rather than global optimum.
• The results depend on the initial cluster assignment of each observation.
  • Run the algorithm multiple times, then select the one producing the smallest within-cluster variation.
• Standardize the data so that distance is not affected by variable unit.

• What is within-cluster variation? I avoid using mathematical formula. But the idea is if the data points in the same group are very close to their group mean, their within-cluster variation will be small.
• We will have K within-cluster variation, one for each group.
• So we hope the sum of K within-cluster variations or the total within-cluster variation is as small as possible.

Source: Introduction to Statistical Learning Fig 12.8

Data for K-Means

df <- read_csv("./data/clus_data.csv")
df  ## income in thousands

# A tibble: 240 × 2
    age income
  <dbl>  <dbl>
1  32.1  167. 
2  59.1   56.9
3  54.0   52.4
4  26.3  -13.9
5  61.3   41.1
6  40.7   39.8
# ℹ 234 more rows

df_clust <- as_tibble(scale(df))
df_clust

# A tibble: 240 × 2
     age income
   <dbl>  <dbl>
1 -0.878  1.00 
2  1.44  -0.601
3  1.00  -0.668
4 -1.38  -1.63 
5  1.64  -0.831
6 -0.137 -0.851
# ℹ 234 more rows

library(factoextra) https://bookdown.org/tpinto_home/Unsupervised-learning/k-means-clustering.html#KM1 https://towardsdatascience.com/k-means-clustering-concepts-and-implementation-in-r-for-data-science-32cae6a3ceba https://www.datanovia.com/en/lessons/k-means-clustering-in-r-algorith-and-practical-examples/ https://uc-r.github.io/kmeans_clustering#optimal https://www.statology.org/k-means-clustering-in-r/

Data for K-Means

df_clust |> ggplot(aes(x = age, 
                       y = income)) + 
    geom_point()

kmeans()

(kclust <- kmeans(x = df_clust, centers = 3))

K-means clustering with 3 clusters of sizes 67, 88, 85

Cluster means:
    age income
1 -0.29   1.33
2  1.04  -0.32
3 -0.85  -0.71

Clustering vector:
  [1] 1 2 2 3 2 3 2 3 1 2 2 3 3 2 3 3 1 3 1 1 3 3 3 2 3 3 2 2 3 1 3 2 1 1 2 1 3
 [38] 3 3 1 3 3 2 1 3 1 2 3 2 2 2 3 1 3 2 3 3 2 1 2 2 3 2 2 2 3 3 2 3 2 2 3 1 1
 [75] 3 2 3 2 2 3 2 2 3 2 1 1 1 2 2 2 3 3 3 3 1 2 1 3 3 2 3 3 2 3 1 2 2 3 1 1 1
[112] 2 1 2 2 2 2 3 2 2 2 1 3 1 3 2 2 2 1 1 2 1 3 2 3 1 1 1 1 3 2 1 1 3 3 3 2 2
[149] 3 2 1 2 1 3 1 3 2 3 1 2 2 1 3 3 3 2 2 1 3 3 2 3 1 1 2 3 2 3 1 3 1 3 1 2 3
[186] 2 2 1 2 2 2 1 3 2 2 2 2 1 1 1 2 1 1 3 1 3 3 1 2 1 3 3 2 2 1 3 3 3 2 1 2 1
[223] 2 3 3 3 2 1 3 1 1 1 3 2 2 2 1 3 3 1

Within cluster sum of squares by cluster:
[1] 66 41 39
 (between_SS / total_SS =  69.5 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"      

kmeans()

kclust$centers

    age income
1 -0.29   1.33
2  1.04  -0.32
3 -0.85  -0.71

kclust$size

[1] 67 88 85

head(kclust$cluster, 20)

 [1] 1 2 2 3 2 3 2 3 1 2 2 3 3 2 3 3 1 3 1 1

Cluster Info

(df_clust_k <- augment(kclust, df_clust))

# A tibble: 240 × 3
     age income .cluster
   <dbl>  <dbl> <fct>   
1 -0.878  1.00  1       
2  1.44  -0.601 2       
3  1.00  -0.668 2       
4 -1.38  -1.63  3       
5  1.64  -0.831 2       
6 -0.137 -0.851 3       
# ℹ 234 more rows

(tidy_kclust <- tidy(kclust))

# A tibble: 3 × 5
     age income  size withinss cluster
   <dbl>  <dbl> <int>    <dbl> <fct>  
1 -0.286  1.33     67     65.9 1      
2  1.04  -0.325    88     40.8 2      
3 -0.848 -0.714    85     38.9 3      

augment adds the point classifications to the original data set:

K-Means in R

• Clustering Result
• Code

• Steady-income family
• New college graduates/mid-class young family
• High socioeconomic class

df_clust_k |>  
    ggplot(aes(x = age, 
               y = income)) + 
    geom_point(aes(color = .cluster), 
               alpha = 0.8) + 
    geom_point(data = tidy_kclust |>  
                   select(1:2),
               size = 8,
               fill = "black",
               shape = "o") +
    theme_minimal() +
    theme(legend.position = "bottom")

K-Means in R: factoextra

library(factoextra)
fviz_cluster(object = kclust, data = df_clust, label = NA) + 
    theme_bw()

Choose K: Total Withing Sum of Squares

## wss = total within sum of squares
fviz_nbclust(x = df_clust, FUNcluster = kmeans, method = "wss",  
             k.max = 10)

Practical Issues

• Try several different \(K\)s, and look for the one with the most useful or interpretable solution.

Clustering is not beneficial for decision making or strategic plan if the clusters found are not meaningful based on their features.

• The clusters found may be heavily distorted due to outliers that do not belong to any cluster.

• Clustering methods are not very robust to perturbations of the data.

23-K means Clustering

In lab.qmd ## Lab 24 section,

1. Install R package palmerpenguins at https://allisonhorst.github.io/palmerpenguins/

2. Perform K-Means to with \(K = 3\) to cluster penguins based on bill_length_mm and flipper_length_mm of data peng.

library(palmerpenguins)
peng <- penguins[complete.cases(penguins), ] |> 
    select(flipper_length_mm, bill_length_mm)

sklearn.cluster

sklearn.cluster.KMeans

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

df_clus = pd.read_csv('./data/clus_data.csv')

scaler = StandardScaler()
X = scaler.fit_transform(df_clus.values)

kmeans = KMeans(n_clusters=3,  n_init=10).fit(X)

kmeans.labels_[0:10]

array([0, 2, 2, 1, 2, 1, 2, 1, 0, 2], dtype=int32)

np.round(kmeans.cluster_centers_, 2)

array([[-0.29,  1.33],
       [-0.85, -0.72],
       [ 1.04, -0.33]])